Numerojärjestelmät ja ehdot

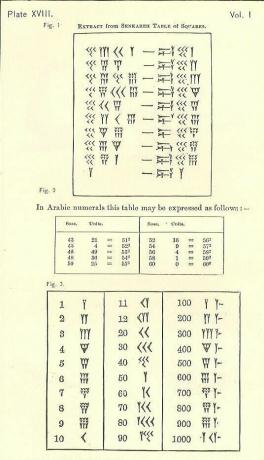
Kolme pääaluetta, jotka eroavat numeroistamme

Kuvittele, kuinka paljon helpompaa olisi oppia aritmeettista varhaisvuosina, jos sinun olisi tehtävä vain kirjoittaa rivi kuten minä ja kolmio. Se on pohjimmiltaan kaikkien Mesopotamian muinaisten ihmisten piti tehdä, vaikka he muuttivat niitä täällä ja siellä, venyttämällä, kääntämällä jne.

Heillä ei ollut kynäämme ja kyniämme tai paperia asiasta. He kirjoittivat työkalun, jota voitaisiin käyttää veistoksessa, koska väline oli savea. Onko tämä vaikeampaa tai helpompaa oppia käsittelemään kuin lyijykynä, se on haaste, mutta toistaiseksi he ovat eteenpäin helppousosastolla, ja vain kaksi perussymbolia on opittava.

Seuraava vaihe heittää jakoavaimen yksinkertaisuusosastolle. Käytämme a Pohja 10, käsite, joka näyttää itsestään selvältä, koska meillä on 10 numeroa. Meitä on tosiasiassa 20, mutta oletetaan, että meillä on sandaalit, joissa on suojaavat varpaasuojat pitääksemme hiekan pois autiomaa, kuuma samasta auringosta, joka leipoo savitabletit ja säilyttää ne meille vuosituhansien ajan myöhemmin. Babylonialaiset käyttivät tätä perustaa 10, mutta vain osittain. Osittain he käyttivät Base 60: tä, samaa numeroa kuin me näemme ympärillämme minuutteina, sekunteina ja kolmion tai ympyrän asteina. He olivat taitavia tähtitieteilijöitä, joten lukumäärä olisi voinut saada heidän havainnoistaan ​​taivaasta. Pohjassa 60 on myös useita hyödyllisiä tekijöitä, joiden avulla on helppo laskea. Silti se, että sinun täytyy oppia Base 60, on pelottava.

Kohdassa "Homoge to Babylonia" [Matemaattinen lehti, Voi. 76, nro 475, "Matematiikan historian käyttö matematiikan opetuksessa" (maaliskuu 1992), s. 1 158-178], kirjailija-opettaja Nick Mackinnon sanoo käyttävänsä babylonialaista matematiikkaa opettamaan 13-vuotiaille muille kuin kymmenelle emäkselle. Babylonian järjestelmä käyttää base-60: tä, mikä tarkoittaa, että sen sijaan, että desimaaliluku olisi desimaalin tarkkuudella, se on seksimaalinen.

Sekä Babylonian lukujärjestelmä että meidän luottamuspaikkamme antavat lisäarvoa. Kaksi järjestelmää tekevät sen eri tavalla, osittain siksi, että niiden järjestelmästä puuttui nolla. Babylonian vasemmalta oikealle (korkeasta matalaan) -asennusjärjestelmän oppiminen perusaritmeetian ensimmäisen maun kannalta ei todennäköisesti enää ole vaikeaa kuin 2-suuntaisen oppiminen, jossa meidän on muistettava desimaalilukujen järjestys - desimaalilukuna kasvaen, niitä, kymmeniä, satoja, ja sitten leikitellessä toiseen suuntaan toisella puolella, ei oneths-saraketta, vain kymmenesosa, sadasosa, tuhannesosa jne.

Käsittelen Babylonian järjestelmän asemia muilla sivuilla, mutta ensin on joitain tärkeitä lukusanoja, jotka on opittava.

Puhumme vuosien jaksoista desimaalimäärien avulla. Meillä on vuosikymmen 10 vuotta, vuosisata 100 vuotta (10 vuosikymmentä) tai 10X10 = 10 vuotta neliössä, ja vuosituhat on 1000 vuotta (10 vuosisataa) tai 10X100 = 10 vuotta kuutiometriä. En tiedä yhtään korkeampaa termiä, mutta ne eivät ole yksiköitä, joita babylonialaiset käyttivät. Nick Mackinnon viittaa Sir Henry Rawlinsonin (1810-1895) * Senkarehin (Larsa) tablettiin yksiköissä, joita babylonialaiset käyttivät, ei vain kyseisten vuosien, vaan myös ilmoitettujen määrien osalta:

1. Soss
2. ner
3. sar.

sossnersosssarsoss

Vielä ei tie-katkaisija: Ei ole välttämättä mitään helpompaa oppia johdettu neliö- ja kuutiovuositermit latinaksi kuin se on yhden tavun babylonialaisia, joihin ei liity kuutiotusta, vaan kertolaskua 10.

Mitä mieltä sinä olet? Olisiko numeron perusteiden oppiminen ollut vaikeampaa Babylonian koululaisena tai nykyaikaisena oppilaana englanninkielisessä koulussa?

* George Rawlinson (1812-1902), Henryn veli, näyttää yksinkertaistetun transkriboidun neliötaulukon Muinaisen itämaailman seitsemän suurta monarkiaa. Taulukko näyttää olevan tähtitieteellinen, perustuen Babylonian vuosiluokkiin.

Kaikki valokuvat ovat peräisin tästä online-skannatusta versiosta 1800-luvun George Rawlinson's -julkaisusta Muinaisen itämaailman seitsemän suurta monarkiaa.

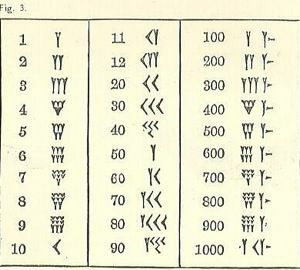
Koska olemme kasvaneet eri järjestelmällä, babylonialaiset numerot ovat hämmentäviä.

Ainakin numerot alkavat korkealta vasemmalta alhaalta oikealle, kuten arabialainen järjestelmämme, mutta loput vaikuttavat todennäköisesti vierailta. Yhden tunnus on kiila tai Y-muoto. Valitettavasti Y edustaa myös 50: tä. On olemassa muutamia erillisiä symboleja (kaikki perustuvat kiilaan ja viivaan), mutta kaikki muut numerot muodostetaan niistä.

Muista, että kirjoitusmuoto on nuolenpääkirjoitus tai kiilamainen. Viivojen piirtämiseen käytetyn työkalun vuoksi valikoima on rajoitettu. Kiilalla voi olla pyrstö, joka on vedetty vetämällä cuneiform-kirjoituskynä savea pitkin osan kolmiomallin jäljennöksen jälkeen.

10, jota kuvataan nuolenpäänä, näyttää vähän kuin

Kolme riviä, joissa on enintään 3 pientä 1: tä (kirjoitettu kuten Y, joissa on lyhennettyjä häntä) tai 10 s (10 on kirjoitettu kuten

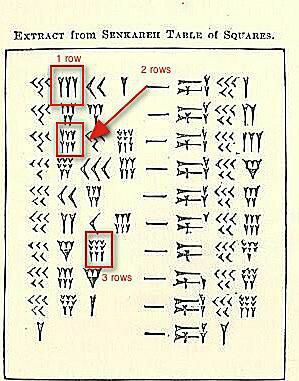
Cuneiform-numeroita on kolme klusterit korostettu yllä olevassa kuvassa.

Tällä hetkellä emme ole kiinnostuneita heidän arvosta, vaan osoittamisesta, kuinka näkisit (tai kirjoitat) missä tahansa 4 - 9 samaa numeroa ryhmiteltynä. Kolme menee peräkkäin. Jos on neljäs, viides tai kuudes, se menee alle. Jos siellä on seitsemäs, kahdeksas tai yhdeksäs, tarvitset kolmannen rivin.

Seuraavilla sivuilla jatketaan ohjeita laskelmien suorittamisesta Babylonian koveriformilla.

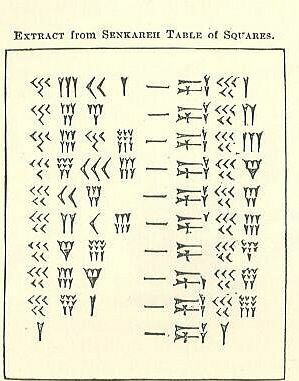
Mitä olet lukenut yllä aiheesta Soss - joka muistat, on babylonialainen 60 vuoden ajan, kiila ja nuolenpää - jotka ovat kuvionmuotoisia merkkejä kuvaavat, katso jos pystyt selvittämään kuinka nämä laskelmat toimivat. Viivamaisen merkinnän toinen puoli on numero ja toinen on neliö. Kokeile sitä ryhmänä. Jos et pysty selvittämään sitä, katso seuraava vaihe.

Voitko selvittää sen nyt? Anna sille mahdollisuus.

...

Vasemmalla puolella on 4 selkeää saraketta, jota seuraa viivamainen merkki ja 3 saraketta oikealla. Vasemmalta puolelta 1s-sarakkeen vastaavuus on oikeastaan ​​kaksi saraketta, jotka ovat lähinnä "viivaa" (sisäsarakkeet). Muut 2 ulompaa saraketta lasketaan yhdessä 60-luvun sarakkeeksi.

• 4-
• 3-Y = 3.
• 40+3=43.
• Ainoa ongelma on, että heidän takanaan on toinen numero. Tämä tarkoittaa, että ne eivät ole yksiköitä (niiden paikka). 43 ei ole 43-yksi, vaan 43-60, koska se on seksuaalinen (base-60) -järjestelmä ja se on Soss sarake, kuten alempi taulukko osoittaa.
• Kerro 43: lla 60: lla saadaksesi 2580.
• Lisää seuraava numero (2-
• Sinulla on nyt 2601.
• Se on 51: n neliö.

Seuraavassa rivissä on 45 Soss sarakkeessa, joten kerrotaan 45 60: llä (tai 2700) ja lisätään sitten 4 yksiköiden sarakkeesta, niin että sinulla on 2704. 2704: n neliöjuuri on 52.

Voitko selvittää, miksi viimeinen numero = 3600 (60 neliötä)? Vihje: Miksi se ei ole 3000?